Applications des fonctions usuelles à la physique

Mouvement dans un champ de force centrale newtonien

Deuxième principe de la thermodynamique

Distance de l’horizon en fonction de l’altitude

On peut déjà noter l'utilité des fonctions exponentielles pour le circuit RLC mais aussi pour les calculs d'aire et de surface, la loi de Biot et Savart mais il existe d'autres exemples d'applications:

Mouvement dans un champ de force centrale newtonien

Introduction

Soient deux points matériels A(m_A,q_A) et B(m_B,q_B).
$\overrightarrow{f_{\mathrm{AB}}}=-\frac{G{m}_A{m}_B}{r²}\overrightarrow{u_{\mathrm{AB}}}=>E_p=-\frac{G{m}_A{m}_B}{r}$
$\overrightarrow{f_{\mathrm{AB}}}=\frac{q_A{q}_B}{4\pi {\xi }_{0}r}\overrightarrow{u_{\mathrm{AB}}}=>E_p=\frac{q_A{q}_B}{4\pi {\xi }_{0}r}$ Tout se passe comme s'il n'y avait qu'un poids M(µ) soumis a un champ de force centrale (vers G), G le barycentre du système {A(m_A),B(m_B)}
On pose $E_p=\frac{k}{r}$ avec k = $\{\begin{array}{c}\frac{q_A{q}_B}{4\pi {\xi }_0}\\ -G{m}_A{m}_B\end{array}$
On réalise l'étude dans le référentiel barycentrique R galliléen.

Trajectoire générale

On applique le Principe Fondamental de la Dynamique dans R à M de masse réduite µ.
$\mu \overrightarrow{a}=\frac{k}{r²}\overrightarrow{u_r}$
De cette équation il est possible d'en déduire l'équation suivante :
$r\; =\frac{p}{e\cos (\theta -{\theta }_0)-\xi }$ Il s'agit de l'équation générale des coniques.
θ₀ correspond à la direction de l'axe focal. Ce qui détermine le mouvement de M, donc A et B ont le même mouvement que M.
Si

• e=0 il s'agit d'un cercle,
  
  by CALLAUD Pierre
• 0 < e < 1 il s'agit d'une ellipse,
  
  by CALLAUD Pierre
• e=1 il s'agit d'une parabole,
  
  by CALLAUD Pierre
• e>1 il s'agit d'une hyperbole.
  
  by CALLAUD Pierre

Deuxième principe de la thermodynamique

Enoncé

Pour tout système thermodynamique il existe une fonction appelée entropie S telle que :

1. S est extensible,
2. S est une fonction d'état : à l'équilibre thermodynamique, S ne dépend que d'un petit nombre de paramètres d'état, indépendants du chemin suivi.
3. Au cour de l'évolution d'un système fermé et calorifugé d'un état initial Ei à un état final Ef, l'entropie ne peut qu'augmenter. $\mathrm{\Delta S}\ge 0$

Identités thermodynamiques

On a l'égalité suivante : dU = TdS+PdV Avec U l'énergie interne définie par le premier principe de la thermodynamique, T la température du système, P sa pression, V son volume. On a aussi l'égalité similaire pour l'enthalpie interne H : dH = TdS + VdP

Variation d'entropie au cours d'une transformation réversible

Pour une transformation réversible on a : $dS=\frac{\mathrm{\delta Q}}{T}$ Et si en plus le système est calorifugé on a alors ΔS = 0.

Entropie de quelques fluides modèles

Phase condensée incompressible

Dans ce cas $\delta Q\; =\; CdT$ car la propriété d'une phase condensée est un volume constant.
donc $dS=\frac{\mathrm{CdT}}{T}$ Soit en intégrant entre la température initiale Ti et la température finale Tf $\Delta S=Cln(\frac{\mathrm{Tf}}{\mathrm{Ti}})$

Gaz parfait

Pour un gaz parfait on a : $PV=nRT\; et\; dU\; =\; \delta Q\; -PdV\; =\; CvdT$
d'où $\delta Q=CvdT+PdV$ ainsi $dS=\frac{\mathrm{CvdT}}{T}+\frac{\mathrm{PdV}}{T}$ Et comme $\frac{P}{T}=\frac{\mathrm{nR}}{V}$ $dS=\frac{\mathrm{CvdT}}{T}+\frac{\mathrm{nRdV}}{V}$ Donc en intégrant entre l'état final et l'état initial nous obtenons $\Delta S\; =Cvln(\frac{\mathrm{Tf}}{\mathrm{Ti}})\; +\; nRln(\frac{\mathrm{Vf}}{\mathrm{Vi}})$

Gaz de Van Der Waals

Pour ce type de gaz on a : $\Delta S=Cvln(\frac{\mathrm{Tf}}{\mathrm{Ti}})+nRln(\frac{\mathrm{Vf-nb}}{\mathrm{Vi-nb}})$ b n'est en fait qu'un terme correcteur de l'idéalité des gaz parfait pour se rapprocher de la réalité.

Distance de l’horizon en fonction de l’altitude

On peut se demander à quelle distance se trouve l’horizon en fonction de l’altitude à laquelle se trouve l’observateur (L, la longueur de l’arc de cercle en bleu sur la figue en dessous)

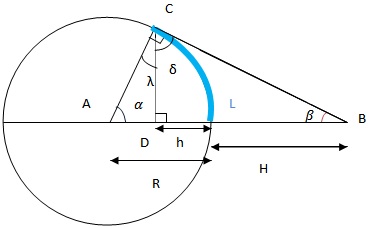
COHU Aurélien

On suppose que la terre est une sphère parfaite de rayon R
On cherche à déterminer L en fonction de la hauteur H.
Par définition d'un angle, $\alpha =\frac{L}{R}$ d'où : $L=\alpha R$
On cherche donc par trigonométrie à exprimer $\alpha$
La droite (BC) est tangente au cercle représentant la terre car C est le point le plus éloigné visible, il est par définition unique et une droite coupant un cercle en un seul point est par définition une tangente au cercle.
Donc (AC) et (BC) sont perpendiculaire. D'où le triangle ABC est rectangle en C.
Donc $sin(\beta )=\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{R}{R+H}$
Et donc $\beta =Arcsin\; (\frac{R}{R+H}$)
Or, $\alpha =\frac{\pi }{2}-\lambda \; ,\; \lambda \; =\frac{\pi }{2}-\; r\; ,\; r=\frac{\pi }{2}-\beta$
Donc $\alpha \; =\frac{\pi }{2}-\beta \; =\frac{\pi }{2}-\; Arcsin\; (\frac{R}{R+H})=\; Arccos(\frac{R}{R+H})$ (Rappel : Arcsin(x)+ Arccos(x)=$\frac{\pi }{2}$ Cf. exercice 2)
Donc $L=R\; Arccos(\frac{R}{R+H})$









Ce(tte) oeuvre est mise à disposition selon les termes de la Licence Creative Commons Paternité - Pas d'Utilisation Commerciale 3.0 France.