$Les MATH pas a pas$

Applications des intégrales à la physique

Calcul de volumes et de surfaces

Prenons ici l'exemple d'une sphère et d'une boule de rayon égal à un. On se place dans un système de coordonnées sphériques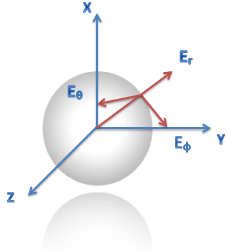

by CALLAUD Pierre

L'élément de volume dans ce système de coordonnées est :

dV=r²sin(θ)dθdΦdr

L'élément de surface dans ce systéme de coordonnées est :

dS=r²sin(θ)dθdΦ

Pour déterminer le volume et la surface d'une sphère il faut intégrer ces éléments de volume et de surface. Pour le volume il s'agit d'une intégrale triple et pour la surface il s'agit d'une intégrale double.

$V=\int_{0}^{1}\int_{0}^{2\pi}\int_{0}^{\pi}r^2 sin(\theta )d\theta d\Phi dr$

=[\frac{r^{3}}{3}]_{0}^{1} [\cos θ]_{0}^{π} 2 π

= \frac{4}{3} π

$S=\int_{0}^{2\pi}\int_{0}^{\pi}r^2 sin(\theta )d\theta d\Phi$

= r² [\cos θ]_{0}^{π} 2 π

=4π

Ici nous avons choisi des exemples facils mais on peut généraliser ces calcules pour les calculs de masse non homogène et autre.

La loi de Biot et Savart

En physique, l’application de la loi de Biot et Savart est un bon exemple de calcul d’intégrale.
Rappel : La loi de Biot et Savart
$\vec{B}=\int \frac{\mu _{0}I}{4\pi r^2}\vec{dl}\wedge \vec{u}$

Exemple : le fil infini

On va calculer le champ magnétique pour un fil infini parcourue par un courant I constant. Le fil est selon l’axe x.

by CALLAUD Pierre

D’après la loi de Biot et Savart, on a
$\vec{B}=\int \frac{\mu _{0}I}{4\pi r^2}\vec{dl}\wedge \vec{PM}$
On trouve alors que :
cos(θ)=

\frac{r}{PM} \Rightarrow PM = r \cos (θ)

tan(θ) = \frac{l}{r} \Rightarrow l = r \tan (θ) \Rightarrow \vec{dl} = \frac{r}{\cos ² (θ)} dθ \vec{u_{x}}

\vec{PM}

= -PM cos(θ)

\vec{u_{z}}

+PM sin(θ)

\vec{u_{x}}

D'où

\vec{dl} ∧ \vec{PM} = \frac{rPMdθ}{\cos (θ)} \vec{u_{x}}

Puis en remplaçant chaque terme, on trouve :

$\vec{B}=\frac{\mu_0I}{4\pi}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\vec{dl}\wedge \vec{PM}}{PM^3}$
$=\frac{\mu_0I}{4\pi}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{r^2}{cos^2(\theta)}\frac{cos^3(\theta)}{r^3}d\theta\vec{u_y}$
$=\frac{\mu_0I}{4\pi r}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}cos(\theta)d\theta\vec{u_y}$

= \frac{µ_{0} I}{4 πr} [sin(θ)]_{- \frac{π}{2}}^{\frac{π}{2}} \vec{u_{y}}

Soit

\vec{B} = \frac{µ_{0} I}{2 πr} \vec{u_{y}}

Deuxième loi de Kepler

Nous allons ici démontrer la mois de Kepler:

Enoncé de la loi de Kepler

Soit A(t) l'aire de la surface balayée par le rayon vecteur

\vec{r}

durant le mouvement, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.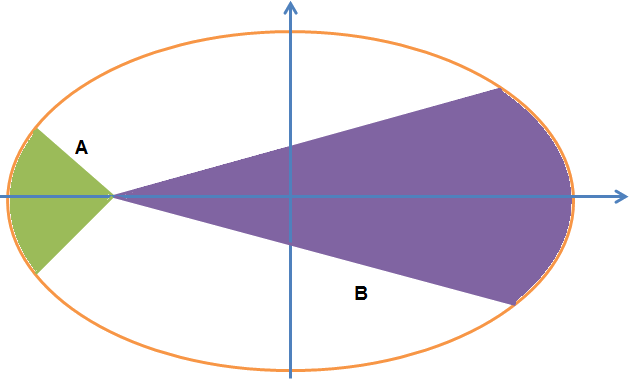

by CALLAUD Pierre

En supposant que pour un même temps les chemins présenté ici sont parcourrus alors A = B (les aires en couleur)
De plus :

A(t)= \frac{| | \vec{L} | |}{2 m} t

Avec m la masse du corps et L le moment cinétique du corps.

Démonstration

D’après la loi de Green-Riemann :
$A(t) = \frac{1}{2}\int_{0}^{t}(x(t)y'(t)-y(t)x'(t))dt$
On remarque que :

x (t) y' (t) - y (t) x' (t)

= x²(t) \frac{d}{dt} (\frac{y (t)}{x (t)}) dt

On obtient :
$A(t) = \frac{1}{2}\int_{0}^{t}x^2 (t)\frac{d}{dt}(\frac{y(t)}{x(t)})dt$
On pose

x(t) = r(t)cos(θ(t))

y(t) = r(t)sin(θ(t))

, on a alors :
$A(t) = \frac{1}{2}\int_{0}^{t}r^2 (t)cos^2(\theta (t))\frac{d}{dt}(tan(\theta (t))dt = \frac{1}{2}\int_{0}^{t}r^2 (t)\frac{d\theta (t)}{dt}dt$
Or, pour une force centrale on a :

r²(t) \frac{dθ}{dt} = \frac{L}{m}

D’où le résultat.

Plus d'explications :

Calcul de volumes et de surfaces

La loi de Biot et Savart

Les lois de Kepler

Retour en haut de la page

Accueil

Crédit

Ce(tte) oeuvre est mise à disposition selon les termes de la Licence Creative Commons Paternité - Pas d'Utilisation Commerciale 3.0 France.