$Les MATH pas a pas$

Les développements limités

1. Formules de Taylor

Les formules de Taylor, du nom du mathématicien Brook Taylor, permettent l'approximation d'une fonction plusieurs fois dérivable au voisinage d'un point par un polynôme dont les coefficients dépendent uniquement des dérivées de la fonction en ce point.

Formule de Taylor avec reste intégral ou formule de Taylor-Laplace

Soit I un ensemble,

f ∈ C^{n + 1} (I, ℝ), n \in ℕ, \forall a, b \in I

$f(b) = \sum_{k=0}^{n}\frac{f^{(k)}(a)}{k!}(b-a)^{k}+\int_{a}^{b}\frac{(b+t)^{n}}{n!}f^{(n+1)}(t)dt$

Inégalité de Taylor-Lagrange

Soit I un ensemble,

f ∈ C^{n + 1} (I, ℝ), n \in ℕ, \forall a, b \in I

alors
$\left |f(b) - \sum_{k=0}^{n}\frac{f^{(k)}(a)}{k!}(b-a)^{k} \right |\leq \frac{\left | b-a \right |^{n+1}}{(n+1)!}M_{n+1}$
Très souvent on prend

M_{n + 1} = \sup ∣ f^{(n + 1)} ∣

Applications

Obtention d'inégalités : Encadrement d'une fonction par des polynômes.
Limites de suites : On peut minorer ou majorer une fonction moins un polynôme par une fonction de limite finie.

Formule de Taylor-Young

Soit I un ensemble,f∈

C^{n} (I,

ℝ) , n∈ℕ, a ∈I,

\forall x \in I

alors
$f(x) = \sum_{k=0}^{n}\frac{f^{(k)}(a)}{k!}(x-a)^{k}+o((x-a)^{n})$
Lorsque a=0 la formule s'écrit :
$f(x) = \sum_{k=0}^{n}\frac{f^{(k)}(0)}{k!}x^{k}+o((x)^{n})$

Applications

Calcul de limites : Principalement lorsque x tend vers 0
Etude locale d'une fonction

2. Développement limité

En physique comme en mathématique, un développement limité d'une fonction au voisinage est une approximation par un polynôme de la fonction en ce point.

Développement limité en 0 : Généralité

Soit I un ensemble, f∈

C^{n} (I, ℝ), n \in ℕ, a∈I

alors il existe un unique polynôme P de degré n tel que : f(x) = P(x) +o(xⁿ) = P(x) + xⁿε avec

lim_{x \to 0} ∣ ε (x) ∣ = 0

Donc un développement limité est unique.
Un développement limité de f en 0 à l'ordre n est noté DL_n(f,0) ou DL_n(0).
P est la partie régulière du DL_n(f,0).

Propriété de base de DL_n(0)

Si f est paire, P est un polynôme pair (tous les termes non nuls sont de degré pair).
Si f est impaire, P est un polynôme impair.

DL_n(0) fondamentaux n∈ℕ

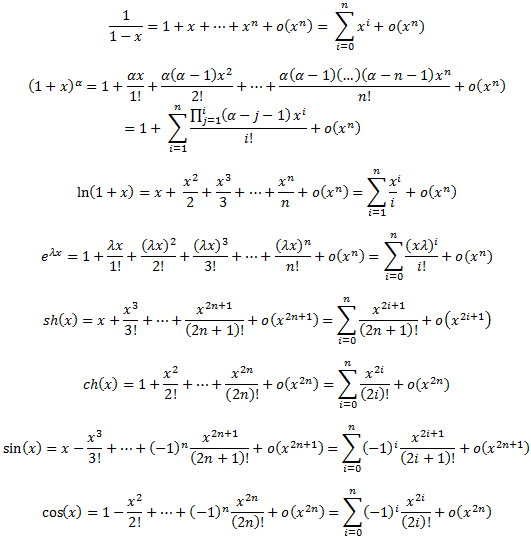
by CALLAUD Pierre

Calcul de DL

Pour calculer un DL_n(f,x₀) on pose t=x-x₀ et g(t) = f(t - x₀) et on calcule un DL_n(g,0).
F possède un DL₀(x₀) si et seulement si F admet une limite finie en x₀ notée L : F(x) + o(1).
(Si F est continue en x₀, L = f(x₀))

F(définie en x₀) possède un DL₁(F,x₀) si et seulement si F dérivable en x₀.
F(x) = F(x₀)+F'(x₀)(x-x₀)+o(x-x₀)

Opération sur les développements limités

Si f(x) = P(x) + o (xⁿ) et g(x) = Q(x) + o (xⁿ) avec P et Q des polynômes de degré n alors

(f+g)(x) = (P+Q)(x)+o(xⁿ)
(gf)(x)=T(x)+o(xⁿ)

Soit u définie au voisinage de 0, avec $lim_{x \to 0} u (x) = 0$ , si u admet un DL_n alors la fonction f= $\frac{1}{1 + u}$ admet aussi un DL_n(0)

Soient f et g définies au voisinage de 0, ayant un DL_n(0), si $\underset{x \to 0}{lim g (x)} = L≠0$ alors $\frac{f}{g}$ admet un DL_n(0).

Intégration des développements limités

Soit

f∈C(I,ℝ)

ayant un DL_n(0) de la forme (n>0) $f(x) = \sum_{k=0}^{n}\frac{a_{k}}{k!}x^{k}+o((x)^{n})$
Toute primitive F de f sur I admet un DL_n+1(f,0) de la forme $F(x) = F(0)+\sum_{k=0}^{n}\frac{a_{k}}{(k+1)!}x^{k+1}+o((x)^{n})$

Dérivation

On ne peut pas toujours dériver le DL_n(f,0) pour obtenir le DL_n+1(f',0), car le lien entre DL et dérivées successives n'est pas réciproque. Cependant si f est de classe Cⁿ sur I alors la dérivation est possible.

La fiche résumée

Retour en haut de la page

Accueil

Crédit