Applications des équations différentielles à la chimie

Cinétique chimique

Chimie nucléaire

Cinétique chimique

Réaction d'ordre 0 à un réactif

Soit la réaction :
A=>B
Condition initiale : [A](t=0)=[A]₀
Définition : une telle réaction d'ordre 0 a une vitesse v=$-\frac{d\left[A\right]}{\mathrm{dt}}$=$\frac{d\left[B\right]}{\mathrm{dt}}$ constante.
Donc $-\frac{d\left[A\right]}{\mathrm{dt}}$=k soit d[A]=-kdt en intégrant entre t=0 et un instant t quelconque on a :
[A]=-kt+[A]₀

Réaction d'ordre 1 à un réactif

Soit la réaction :
A=>B
Conditions initiale : [A](t=0)=[A]₀
Définition : une telle réaction d'ordre 1 a une vitesse de la forme v=k[A].
On a donc l'équation différentielle :
$-\frac{d\left[A\right]}{\mathrm{dt}}$=k[A]
Soit
$\frac{d\left[A\right]}{\left[A\right]}$=-kdt
D'où en intégrant entre t=0 et un instant t quelconque on a :
ln($\frac{\left[A\right]}{{\left[A\right]}_0}$)=-kt donc [A]=[A]₀ e^-kt

Réaction d'ordre 2 à un réactif

Soit la réaction :
A=>B
Condition initiale : [A](t=0)=[A]₀
Définition : une telle réaction d'ordre 2 a une vitesse de la forme v=k[A]².
On a donc l'équation différentielle :
$-\frac{d\left[A\right]}{\mathrm{dt}}$=k[A]²
Soit $\frac{d\left[A\right]}{[A]²}$ =kdt
D'où en intégrant entre t=0 et un instant t quelconque on a :
$\frac{1}{\left[A\right]}-\frac{1}{{\left[A\right]}_0}=\mathrm{kt}$ donc $\left[A\right]=\frac{1}{\mathrm{kt}+\frac{1}{{\left[A\right]}_0}}$

Réaction d'ordre n (n>1) à un réactif

Soit la réaction :
A=>B
Condition initiale : [A](t=0)=[A]₀
Définition : une telle réaction d'ordre n a une vitesse de la forme v=k[A]ⁿ.
On a donc l'équation différentielle :
$-\frac{d\left[A\right]}{\mathrm{dt}}$=k[A]ⁿ
Soit
$\frac{d\left[A\right]}{{\left[A\right]}^n}$ =-kdt
D'où en intégrant entre t=0 et un instant t quelconque on a :
$\frac{1}{{(n+1)\left[A\right]}^{n+1}}-\frac{1}{(n+1){\left[A\right]}_0^{n+1}}$=kt

Exemples cinétiques de réactions

by CALLAUD Pierre

Chimie nucléaire

Définition : la radioactivité est la transformation (ou désintégration) de noyaux instables en d'autres noyaux.
Elle est la plupart du temps acompagnée d'émission de particules (${\beta }^{-},{\beta }^{+},\alpha$) mais aussi de rayonnements électromagnatiques (γ).

L'utilité des équations différentielles se trouve dans la loi de décroissance radioactive.

Définition : L'activité d'un échantillon radioactif (A) correspond au nombre de désintégration par unité de temps, donc A=$-\frac{dN}{dt}$ (1). Avec dN (sans unité) le nombre de noyaux désintégrés au bout d'une durée dt (en s). L'activité A s'exprime en Becquerels (i.e. en nombre de désintégrations par seconde).

La loi de décroissance radioactive nous dit que: l'activité A est proportionnelle au nombre de noyaux radioactifs N.
Soit $\exists \lambda \in {ℝ}^{+}$tels que A =λN (2) (λ la constante radioactive, caractéristique à un noyau radioactif).

En utilisant les équations (1) et (2) on en déduit que λN +$\frac{dN}{dt}$= 0.

D'où N = $N_0{e}^{-\lambda t}$ avec $N_0$ le nombre de noyau radioactif à t = 0.

L'iode 131

Prenons l'exemple de l'iode 131 qui a une période de demi-vie de 8,02 jours soit une constante radioactive λ de 0,783 jours^-1.
Pour 1 µg(=N₀) de l'iode 131 on obtient la courbe suivante :

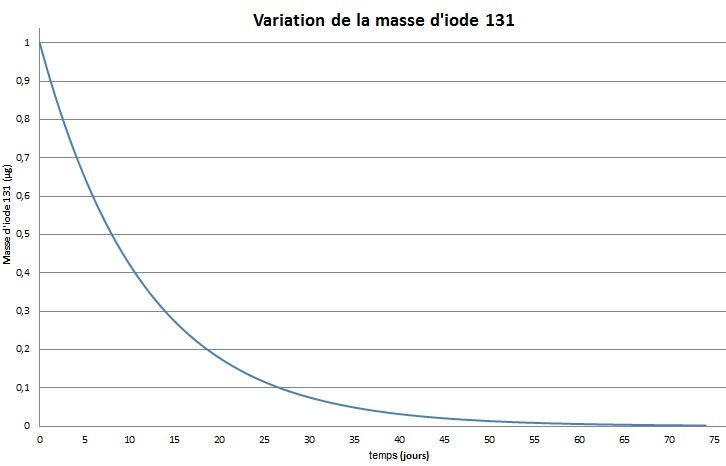
by CALLAUD Pierre

Ce(tte) oeuvre est mise à disposition selon les termes de la Licence Creative Commons Paternité - Pas d'Utilisation Commerciale 3.0 France.