Les Fonctions Trigonométriques

Définitions

Fonctions réciproques

Dérivées des fonctions trigonométriques

Propriétés

1.Définitions

by DEMAZEAU Maxime

Les fonctions trigonométriques les plus couramment utilisées sont le cosinus, le sinus et la tangente. Les fonctions sin et cos sont définies, continues et dérivables sur ℝ et la fonction tan est définie, continue et dérivable sur ╲$\{\frac{\pi }{2}+\mathrm{k\pi }\}$, (k∈ℤ)
Il existe plusieurs façons de définir les fonctions sinus, cosinus et tangente, ici, nous utiliserons une approche graphique.

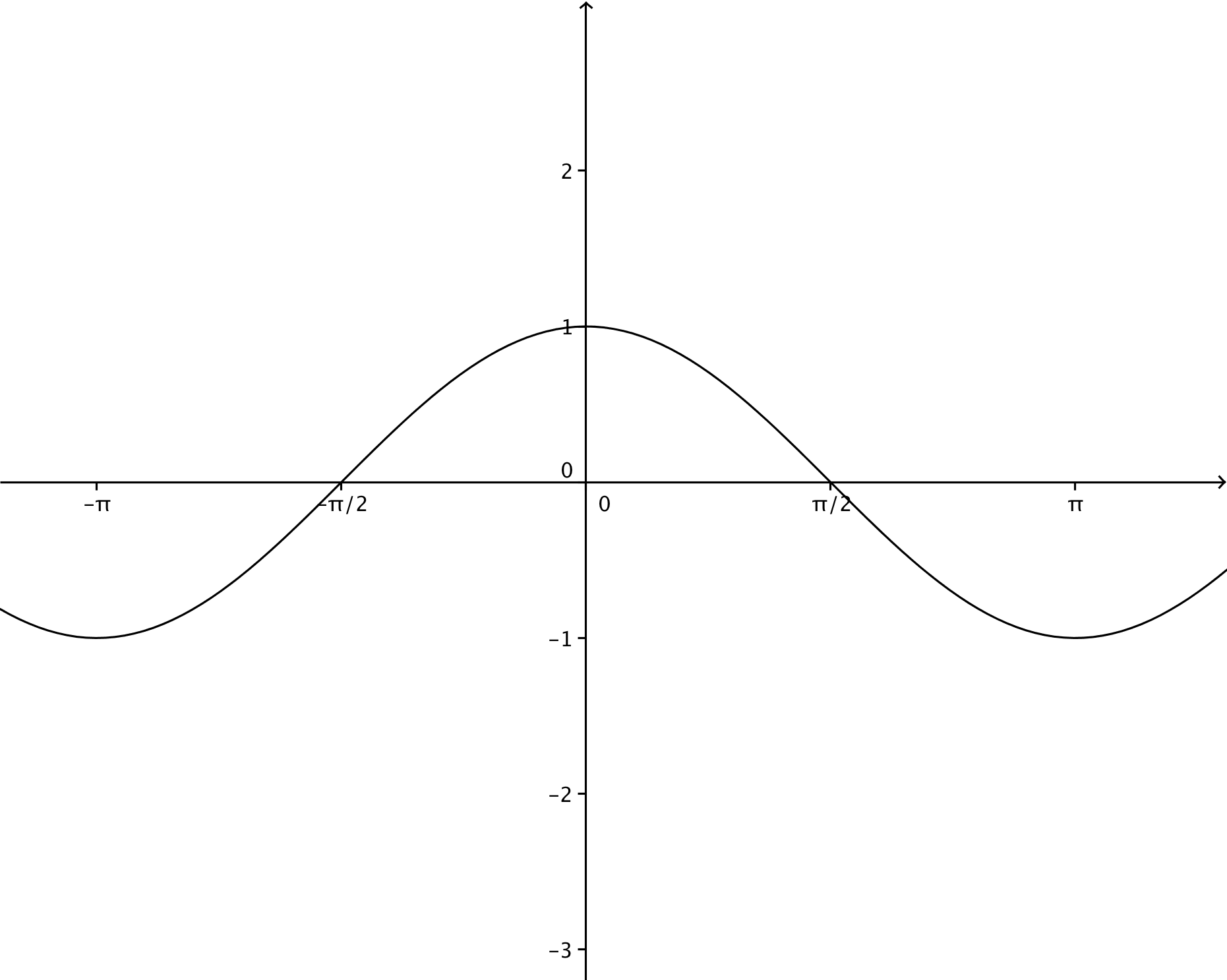
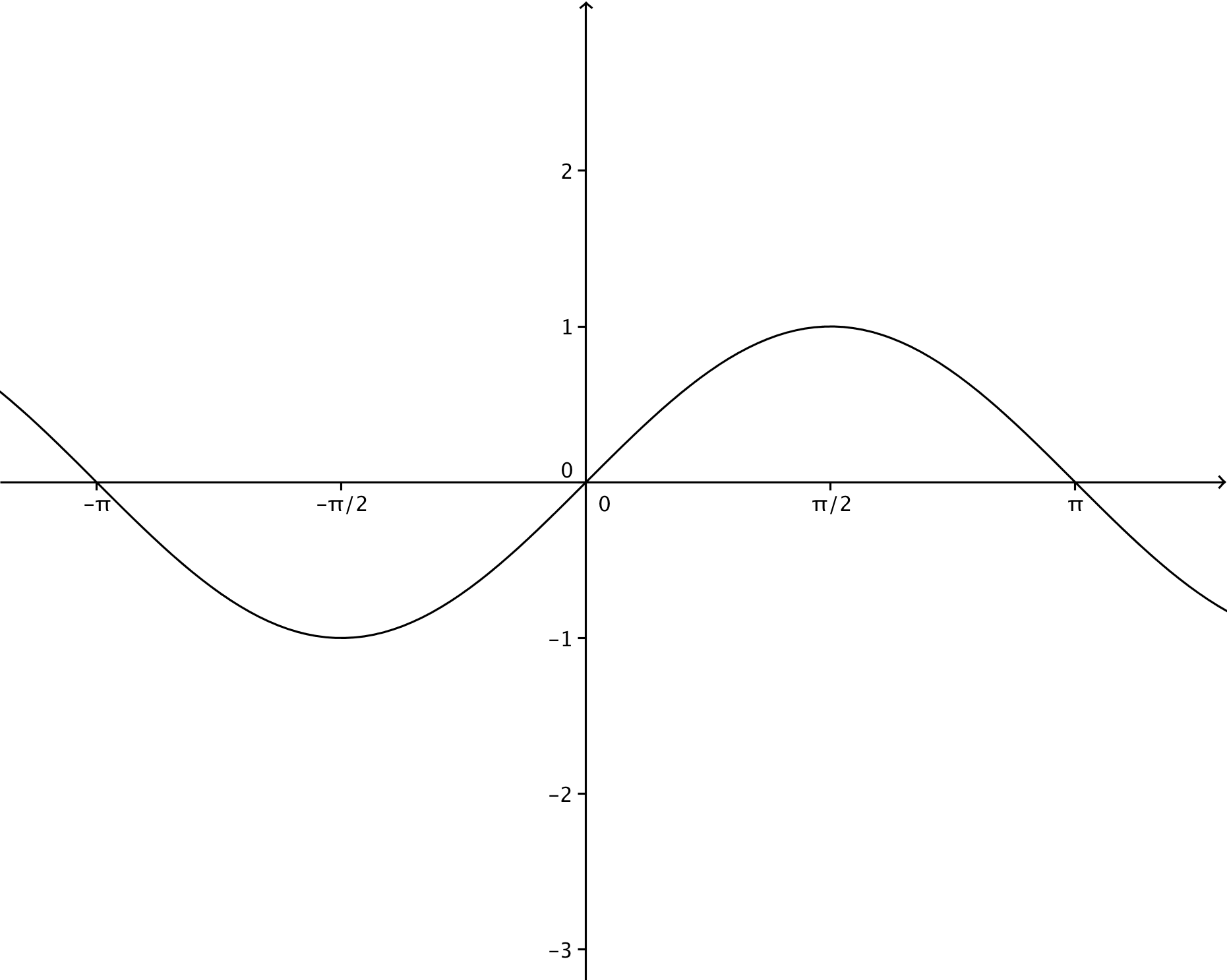
Le cosinus peut être défini comme l’abscisse d’un point sur un cercle de rayon 1 centré à l’origine d’un repère orthonormé et le sinus son ordonnée. L’angle concerné étant celui entre l’axe des x et la droite passant par le point et l‘origine.
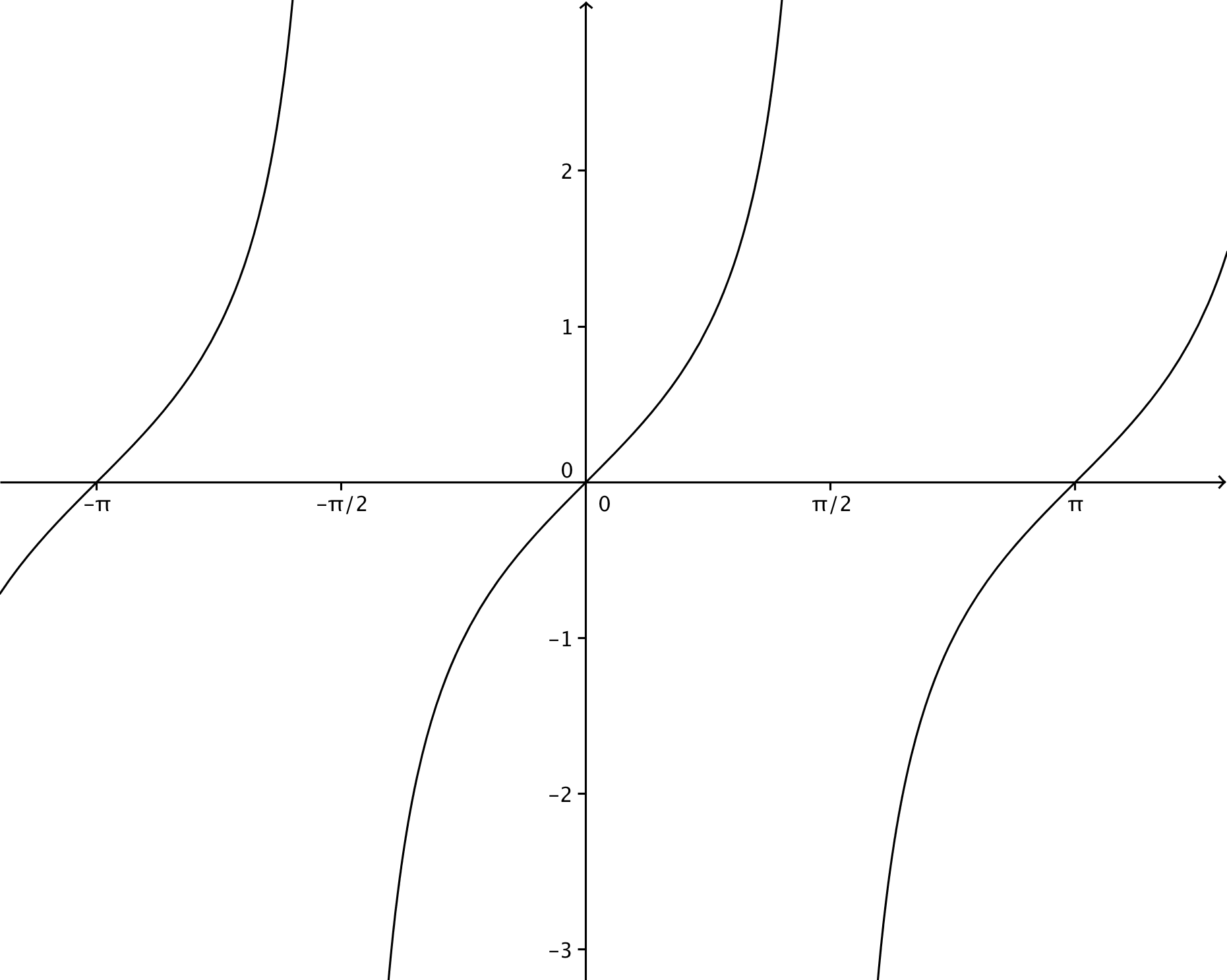
La tangente peut être défini comme l’ordonnée de l’intersection entre la droite passant par le point concerné et l‘origine et la droite x=1.

Représentation graphique :

Cosinus	Sinus	Tangente
by DEMAZEAU Maxime	by DEMAZEAU Maxime	by DEMAZEAU Maxime

2.Fonctions réciproques

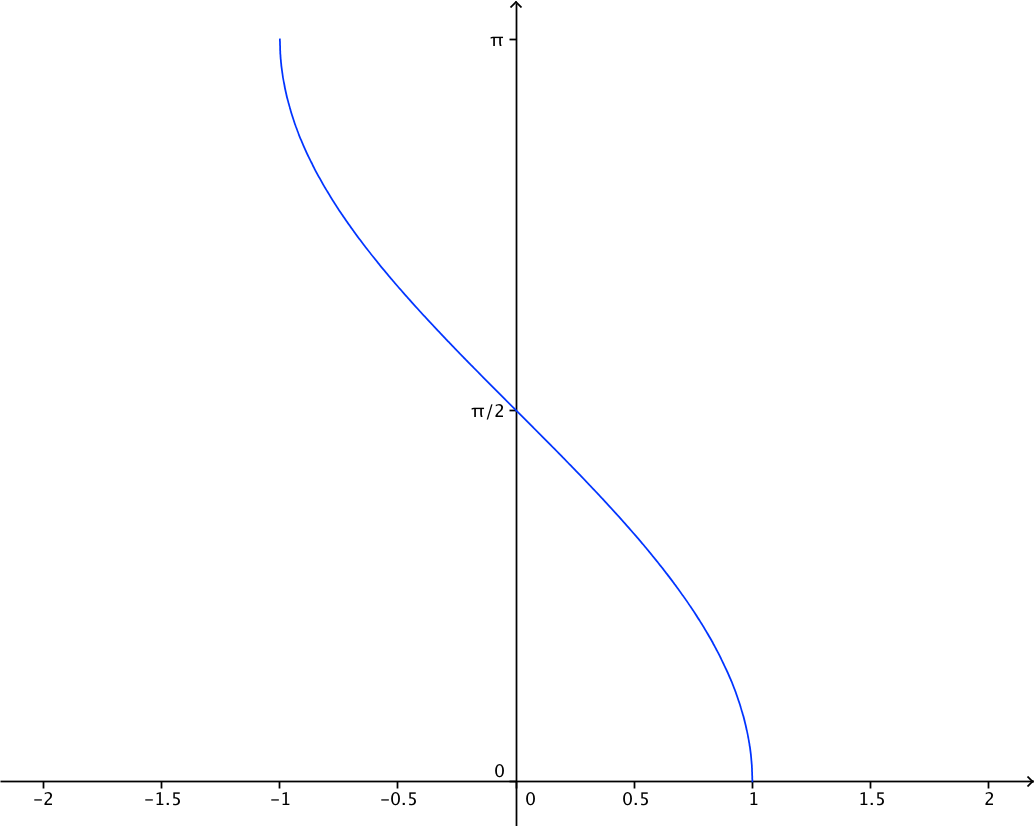
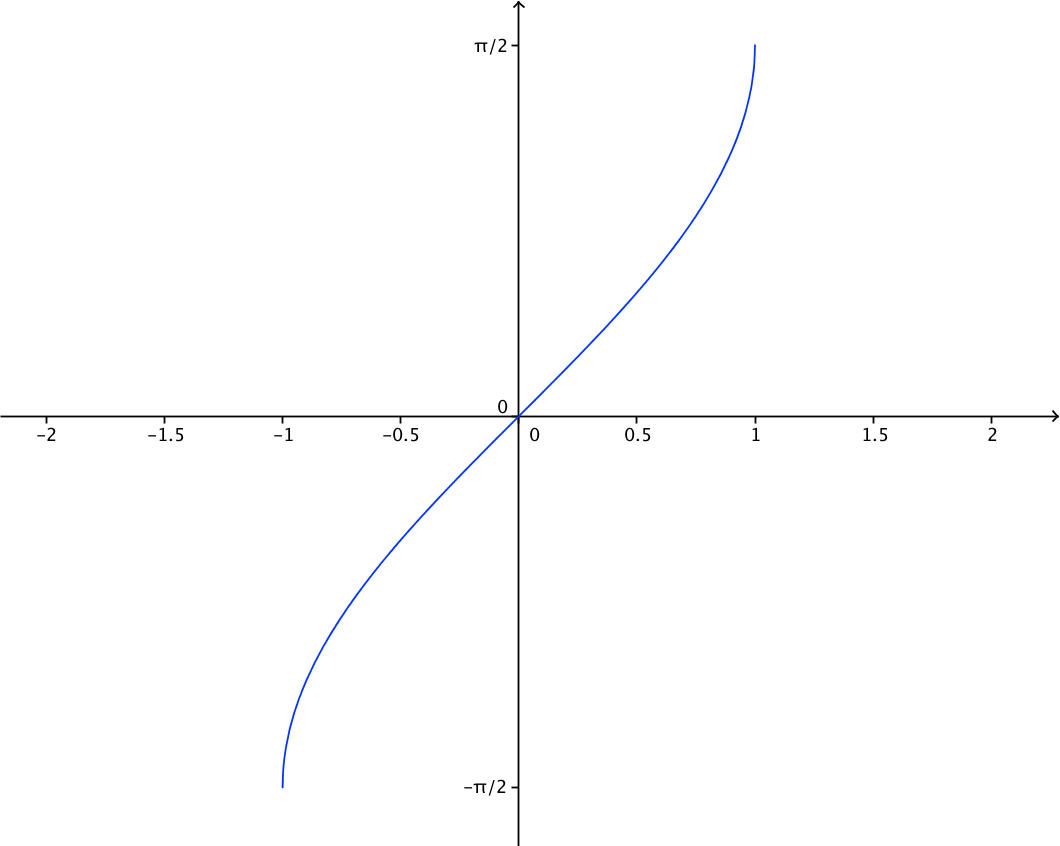
Associées à ces fonctions, existent les fonctions dites trigonométriques réciproques telles que
y=arcsin⁡(x)⟺x=sin⁡(y) (y∈$[-\frac{\pi }{2};\frac{\pi }{2}]$)
y=arccos⁡(x)⟺x=cos⁡(y) (y∈$[-0;\pi ]$)
y=arctan⁡(x)⟺x=tan⁡(y) (y∈$[-\frac{\pi }{2};\frac{\pi }{2}]$)

Représentation graphique :

Arccosinus	Arcsinus	Arctangente
by DEMAZEAU Maxime	by DEMAZEAU Maxime	by DEMAZEAU Maxime

3.Dérivées des fonctions trigonométriques

Toutes les fonctions trigonométriques sont dérivables et on a :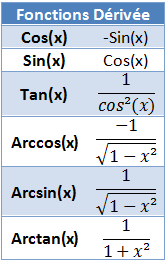

by CALLAUD Pierre

4.Propriétés

by DEMAZEAU Maxime

De l'approche graphique, nous pouvons remarquer quelques propriétés importantes du sinus et du cosinus :

• Leur 2π périodicité
• La parité du cosinus et l’imparité du sinus et les relations suivantes :


cos(a+π)=-cos(a)
sin(a+π)=-sin(a)
cos$(\frac{\pi }{2}-a)$=sin$\left(a\right)$
sin$(\frac{\pi }{2}-a)$=cos$\left(a\right)$
cos$(\frac{\pi }{2}+a)$=-sin$\left(a\right)$
sin$(\frac{\pi }{2}+a)$=cos$\left(a\right)$
cos$(\pi -a)$=-cos(a)
sin$(\pi -a)$=-sin(a)


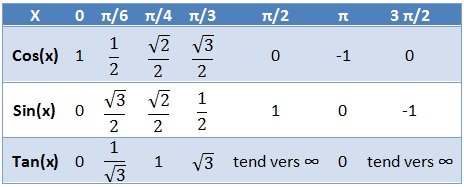
• Leurs valeurs pour quelques angles remarquables :



by CALLAUD Pierre



• Quelque soit x, cos²(x)+ sin²(x)=1.


• D’autres propriétés « calculatoires » des fonctions :

cos⁡(a+b)=cos⁡(a) cos⁡(b)-sin⁡(a) sin⁡(b)
cos⁡(a-b)=cos⁡(a) cos⁡(b)+sin⁡(a) sin⁡(b)
sin⁡(a+b)=sin⁡(a) cos⁡(b)+cos⁡(a)sin⁡(b)
sin⁡(a-b)=sin⁡(a) cos⁡(b)-cos⁡(a)sin⁡(b)
De ces formules, on peut en déduire :
tan$\left(a+b\right)$=$\frac{\tan \left(a\right)+\tan \left(b\right)}{1-\tan \left(a\right)\tan \left(b\right)}$

tan$\left(a-b\right)$=$\frac{\tan \left(a\right)-\tan \left(b\right)}{1+\tan \left(a\right)\tan \left(b\right)}$


cos(p)+cos(q)=2cos$\left(\frac{p+q}{2}\right)$cos$\left(\frac{p-q}{2}\right)$
cos(p)-cos(q)=-2sin$\left(\frac{p+q}{2}\right)$sin$\left(\frac{p-q}{2}\right)$
sin(p)+sin(q)=2sin$\left(\frac{p+q}{2}\right)$cos$\left(\frac{p-q}{2}\right)$
sin(p)-sin(q)=2cos$\left(\frac{p+q}{2}\right)$sin$\left(\frac{p-q}{2}\right)$

(se démontre on posant p=$\frac{a+b}{2}$et q=$\frac{a-b}{2}$)


cos(a)cos(b)=$\frac{1}{2}\left(\cos (a+b)+\cos (a-b)\right)$
sin(a)sin(b)=$\frac{1}{2}\left(\cos (a-b)-\cos (a+b)\right)$
sin(a)cos(b)=$\frac{1}{2}\left(\sin (a+b)\left)\sin \right(a-b)\right)$








Ce(tte) oeuvre est mise à disposition selon les termes de la Licence Creative Commons Paternité - Pas d'Utilisation Commerciale 3.0 France.