Applications des équations différentielles à la physique

Le pendule oscillant

Circuit RLC

Le pendule oscillant

Si on considère le système suivant :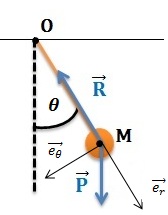

by CALLAUD Pierre

La masse m, de centre de masse M(L,θ) reliée à un fil de masse négligeable, de longueur L, relisé lui-même à un plafond.
On se place dans le référentiel galiléen (O,$\overrightarrow{e_r},$$\overrightarrow{e_{\theta }}$). A t=0 le pendule est làché avec une vitesse initiale nulle et un angle θ non nul. On néglige les frottements de l'aire. En appliquant le principe de conversion de l'énergie, on a Em = Ec + Ep = Constante.

Soit Em = $\frac{\mathrm{mv²}}{2}$ + m.g.cos(θ).L .

En dérivant par rapport à t, on obtient : m.v².v+ m.g.θ'.sin(θ).L = 0 (1).

Or
$\overrightarrow{\mathrm{OM}}=L\overrightarrow{e_{\theta }}$.

Et $\overrightarrow{v}$=$\frac{d\overrightarrow{\mathrm{OM}}}{\mathrm{dt}}$ = Lθ'$\overrightarrow{e_{\theta }}$.

D'où v=Lθ' et v=Lθ''.

Et donc (1) => L²θ'θ''+m.g.θ'.sin(θ).L = 0 => θ''+$\frac{g.\sin \left(\theta \right)}{L}$ =0 (2).

(2) est une équation non linéaire en θ et donc difficilement résolvable, cependant en faisant l'approximation des petits angles on a : sin(θ)=θ.

Ainsi (2) devient
θ''+$\frac{g.\theta }{L}$ =0.

En utilisant la méthode de résolution dans la partie cours on trouve que la solution général de cette équation est de la forme :
θ(t) = Asin(wt)+Bcos(wt) avec w =$\sqrt{\frac{g}{L}}$.

Et comme à t=0 θ(0)=B= θ₀, et v(0)=0=L θ'(0) donc θ'(0)=0 d'où A=0.
Ainsi
θ(t) = θ₀cos (wt).

Circuit RLC

Soit le circuit RLC en série suivant :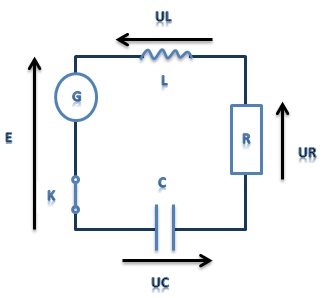

by CALLAUD Pierre

Conditions initiales : UC(0)=0, i(0)=0
D'après la loi des mailles on a : E = UL + UR + UC
Avec :
UL=$\frac{\mathrm{di}}{\mathrm{dt}}$ et UR=Ri
Donc E=UC+Ri+L$\frac{\mathrm{di}}{\mathrm{dt}}$ de plus i=i_c =C$\frac{\mathrm{dUC}}{\mathrm{dt}}$

D'où l'équation différentielle suivante :
E=UC+RC$\frac{\mathrm{dUC}}{\mathrm{dt}}$+LC$\frac{\mathrm{d²}\mathrm{UC}}{\mathrm{d²}t}$

Remarque : UC=E est une solution particulière évidente de cette équation.

Equation homogène :

On divise les tous par LC et on pose y=UC , y'=$\frac{\mathrm{dUC}}{\mathrm{dt}}$ et y''=$\frac{\mathrm{d²}>\mathrm{UC}}{\mathrm{d²}t}$ d'où :

$\frac{y}{\mathrm{LC}}$+$\frac{\mathrm{Ry}\text{'}}{L}$+y''=0
L'équation caractéristique de cette équation a pour déterminant :
Δ=($\frac{\mathrm{R²}}{\mathrm{L²}}-\frac{4}{\mathrm{LC}})$
Trois cas se présentent donc à nous :

• Cas 1 : Δ=0 si R²C-4L=0 =>R=2$\sqrt{\frac{L}{C}}$


• Cas 2 : Δ<0 si R²C-4L<0 =>R<2$\sqrt{\frac{L}{C}}$


• Cas 3 : Δ>0 si R²C-4L>0 =>R>2$\sqrt{\frac{L}{C}}$

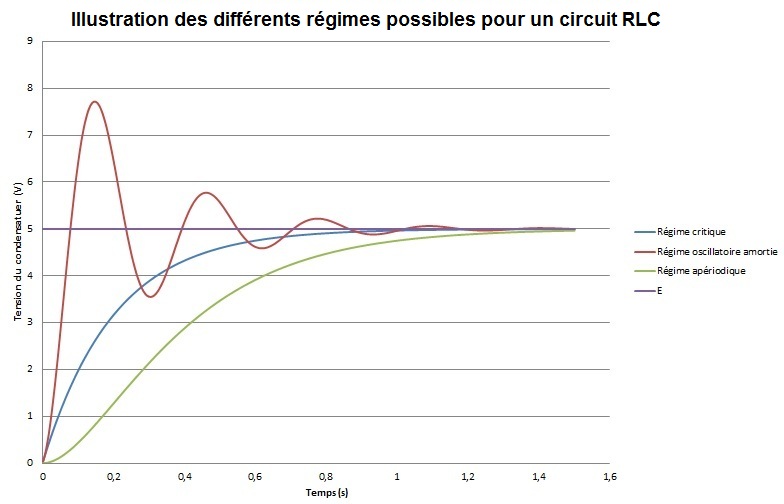
Cas 1 : Régime critique

y=E+(A+Bt)exp(-wt) avec w=$\frac{R}{2L}$
De plus d'après les conditions initiales A=-E car UC(0)=0 et B=0 car i(0)=0
D'où
UC=E(1-exp(-wt))

Cas 2 : Régime oscillatoire amorti

y=E+(Acos(rt+φ))exp(-wt) avec w=$\frac{R}{2L}$ et r=$\frac{\sqrt{-\Delta }}{2}$
De plus d'après les conditions initiales A=-E car UC(0)=0 et φ=0.
D'où
UC=E(1-cos(rt)exp(-wt))

Cas 3 : Régime apèriodique

y=E+Aexp(r₁ t)+Bexp(r₂ t) avec r₁=$\frac{R}{2L}+\frac{\sqrt{\Delta }}{2}$ et r₂=$\frac{R}{2L}-\frac{\sqrt{\Delta }}{2}$
De plus d'après les conditions initiales $\{\begin{array}{c}A+B+E=0\\ A{r}_1+B{r}_2=0\end{array}$ d'ou A=$\frac{E{r}_2}{r_1-r_2}$ et B=$\frac{E{r}_1}{r_1-r_2}$
D'où
UC = E+$\frac{E}{r_1-r_2}\left(r_2\exp \right(r_{1}t)-r_1\exp (r_{2}t\left)\right)$

by CALLAUD Pierre

Ce(tte) oeuvre est mise à disposition selon les termes de la Licence Creative Commons Paternité - Pas d'Utilisation Commerciale 3.0 France.